Os nove pontos da figura estão igualmente espaçados na circunferência. Maria quer pintar alguns desses pontos de tal forma que não exista triângulo equilátero cujos vértices estejam todos pintados. Qual é o maior número de pontos que ela pode pintar?(A) 4 (B) 5 (C) 6 (D 7 (E) 8
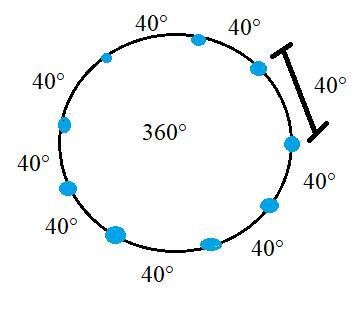
Para resolver esse problema, vamos analisar a condição necessária para evitar a existência de triângulos equiláteros com todos os vértices pintados.
Primeiramente, vamos considerar os possíveis triângulos equiláteros formados pelos pontos. Um triângulo equilátero é aquele em que todos os lados têm o mesmo comprimento e todos os ângulos internos têm a medida de 60 graus.
A travessia de um deserto dura seis dias, e uma pessoa consegue carregar comida
Se pintarmos apenas 3 pontos, formaremos um triângulo equilátero, pois qualquer três pontos adjacentes na circunferência estarão igualmente espaçados. Portanto, pintar apenas 3 pontos não é uma opção viável.
Se pintarmos 4 pontos, formaremos 4 triângulos equiláteros distintos. Podemos escolher 4 pontos adjacentes e pintá-los, mas isso nos deixará com três pontos restantes, formando um triângulo equilátero com esses três pontos. Portanto, pintar 4 pontos também não é uma opção viável.
No entanto, se pintarmos 5 pontos, não será possível formar nenhum triângulo equilátero. Podemos escolher 5 pontos adjacentes e pintá-los, deixando 4 pontos restantes. Não será possível formar um triângulo equilátero com esses 4 pontos, pois sempre haverá uma lacuna entre dois pontos adjacentes que não permitirá a formação de um triângulo equilátero.
Se pintarmos 6 pontos, também não será possível formar um triângulo equilátero. Podemos escolher 6 pontos adjacentes e pintá-los, deixando 3 pontos restantes. Assim como no caso anterior, não será possível formar um triângulo equilátero com esses 3 pontos, pois sempre haverá uma lacuna entre dois pontos adjacentes que não permitirá a formação de um triângulo equilátero.
A partir de 7 pontos pintados, será sempre possível formar um triângulo equilátero. Se escolhermos 7 pontos adjacentes e os pintarmos, deixaremos apenas 2 pontos restantes. Será possível formar um triângulo equilátero com esses 2 pontos e um dos pontos já pintados.
Portanto, o maior número de pontos que Maria pode pintar é 6, pois a partir de 7 pontos pintados será possível formar um triângulo equilátero. Assim, a resposta correta é a alternativa (C) 6.