Resolvendo Problemas Geométricos: Determinando a Área do Triângulo APQ em um Retângulo ABCD
O retângulo ABCD é formado pelos triângulos ABP,CQP, AQD e APQ. As áreas dos triângulos ABP, CQP
e AQD são, respectivamente, 6, 5 e 2 cm². Qual é, em
cm²2, a área do triângulo APQ?
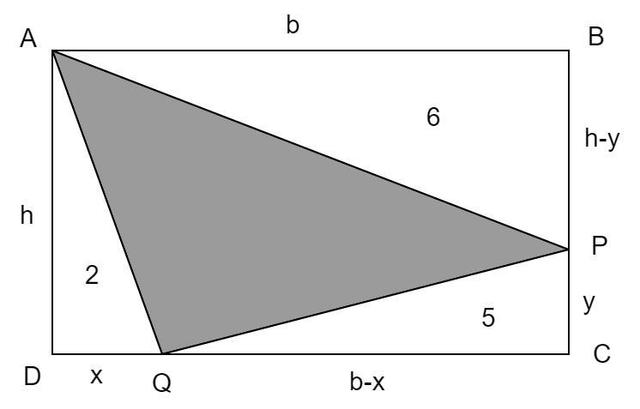
Na resolução de problemas geométricos, o cálculo de áreas desempenha um papel fundamental. Neste artigo, vamos explorar um problema que envolve o retângulo ABCD e os triângulos ABP, CQP, AQD e APQ. O objetivo é determinar a área do triângulo APQ, utilizando fórmulas e relações entre áreas. Acompanhe a solução detalhada a seguir.
Analisando as Relações entre os Triângulos
Para resolver esse problema, é essencial compreender as propriedades do retângulo ABCD e as informações fornecidas. Vamos explorar as áreas dos triângulos ABP, CQP e AQD, que são 6 cm², 5 cm² e 2 cm², respectivamente.
Utilizando a Fórmula da Área do Triângulo
Para calcular a área de um triângulo, utiliza-se a fórmula: área = (base * altura) / 2. Aplicando essa fórmula ao triângulo ABP, obtemos:
Área do Triângulo ABP: 6 cm² = (AB * BP) / 2
Determinando a Área do Triângulo CQP
Analogamente, aplicamos a fórmula da área do triângulo ao triângulo CQP:
Área do Triângulo CQP: 5 cm² = (CQ * PQ) / 2
Encontrando a Área do Triângulo AQD
Seguindo a mesma abordagem, determinamos a área do triângulo AQD:
Área do Triângulo AQD: 2 cm² = (AQ * QD) / 2
Calculando a Área do Triângulo APQ
A área do retângulo ABCD é composta pelos triângulos ABP, CQP, AQD e APQ. Assim, podemos estabelecer a seguinte equação:
Área do Retângulo ABCD = Área do Triângulo ABP + Área do Triângulo CQP + Área do Triângulo AQD + Área do Triângulo APQ
Substituindo as áreas dos triângulos conhecidos, obtemos:
xy = 6 + 5 + 2 + Área do Triângulo APQ
Considerando que xy representa a área do quadrilátero ABCD, podemos afirmar que xy é igual a 24. Portanto:
24 = 13 + Área do Triângulo APQ
Determinando a Área do Triângulo APQ
Isolando a variável Área do Triângulo APQ, encontramos:
Área do Triângulo APQ = 24 – 13 Área do Triângulo APQ = 11 cm²
Confira tambem:
Conclusão
Por meio da análise das propriedades do retângulo ABCD e das informações fornecidas sobre os triângulos ABP, CQP e AQD, conseguimos determinar a área do triângulo APQ como sendo igual a 11 cm². Essa resolução confirma a alternativa correta no gabarito, que é a opção (E) – 11. Ao compreender as relações entre as áreas dos triângulos e utilizar a fórmula da área do triângulo, foi possível resolver o problema de maneira detalhada e precisa. A aplicação desses conceitos geométricos é essencial para o desenvolvimento das habilidades de resolução de problemas e para o entendimento da geometria como um todo. Esperamos que este artigo tenha contribuído para a compreensão do processo de cálculo da área do triângulo APQ e sua relação com o retângulo ABCD.