Por

Um estudo recente revela uma nova abordagem que melhora as previsões de volatilidade do mercado de ações utilizando homologia persistente. Este método aumenta a precisão de vários modelos de previsão, marcando um avanço significativo na integração de topologia e finanças. Crédito: SciTechDaily.com
Em um novo estudo publicado em O Jornal de Finanças e Ciência de Dadosum pesquisador da Escola Internacional de Negócios da Universidade HAN de Ciências Aplicadas, na Holanda, apresentou a teoria da dependência topológica da cauda – uma nova metodologia para prever a volatilidade do mercado de ações em tempos de turbulência.
“A pesquisa preenche a lacuna entre o campo abstrato da topologia e o mundo prático das finanças. O que é verdadeiramente entusiasmante é que esta fusão nos proporcionou uma ferramenta poderosa para melhor compreender e prever o comportamento do mercado bolsista durante tempos turbulentos”, afirmou Hugo Gobato Souto, único autor do estudo.
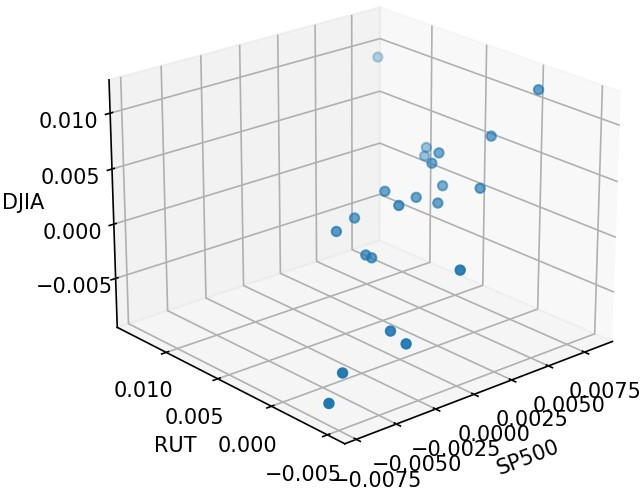
A diferença entre a distância média dos retornos normalizados das ações de dois períodos diferentes pode ser usada como um indicador para prever um período financeiramente turbulento, definindo um valor limite a ser usado durante os períodos normais, uma vez que a distância média é maior durante os períodos normais do que durante os anteriores e períodos turbulentos. No entanto, o problema desta abordagem é o facto de a distância média dos retornos normalizados das ações sofrer a maldição da dimensionalidade e não conseguir detetar relações não lineares e complexas nos dados. A maldição da dimensionalidade que a distância média dos retornos das ações normalizadas sofre é explicada pelo fato de que, à medida que o número de dimensões (ou ações, neste caso) tende ao infinito, a razão entre a distância de quaisquer pontos (digamos A e B) e a distância de quaisquer outros pontos (digamos A e C) se aproxima de 1. Como resultado, a distância média perde o sentido. Por outro lado, a implementação de informações de PH através das normas WD ou L^n de Paisagem Persistente não sofre destes problemas. Portanto, esta é a razão do sucesso da implementação das informações de PH em estudos recentes e da sua escolha neste estudo. Acima está um gráfico de dispersão 3D de 16 de dezembro de 2019 a 16 de janeiro de 2020 (Período Normal). Crédito: Hugo Gobato Souto
Aprimorando as previsões financeiras com homologia persistente
Através de testes empíricos, Souto demonstrou que a incorporação de informações de homologia persistente (PH) aumenta significativamente a precisão de modelos não lineares e de redes neurais na previsão da volatilidade do mercado de ações durante períodos turbulentos.
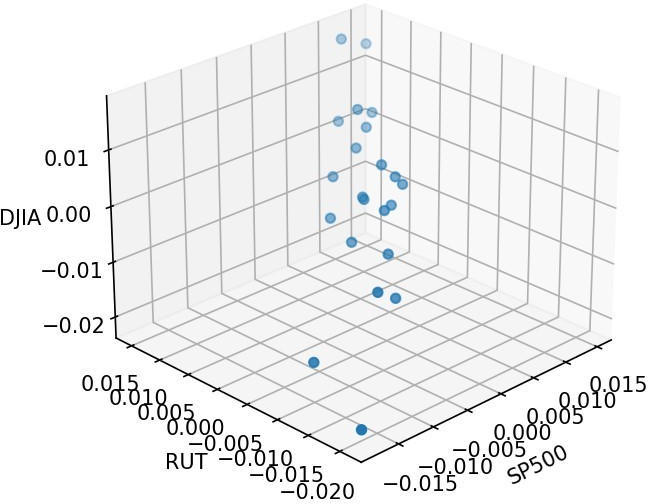
Gráfico de dispersão 3D de 17 de janeiro de 2020 a 19 de fevereiro de 2020 (período anterior). Crédito: Hugo Gobato Souto
“Estas descobertas sinalizam uma mudança significativa no mundo das previsões financeiras, oferecendo ferramentas mais confiáveis para investidores, instituições financeiras e economistas”, acrescentou Souto.
Notavelmente, a abordagem contorna a barreira da dimensionalidade, tornando-a particularmente útil para detectar correlações complexas e padrões não lineares que muitas vezes escapam aos métodos convencionais.
“Foi fascinante observar as melhorias consistentes na precisão das previsões, especialmente durante a crise de 2020”, disse Souto.
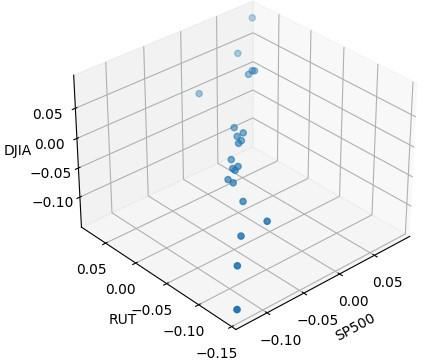
Gráfico de dispersão 3D de 20 de fevereiro de 2020 a 23 de março de 2020 (período turbulento) Crédito: Hugo Gobato Souto
Implicações amplas e direções futuras
As descobertas não se limitam a um tipo específico de modelo. Ele abrange vários modelos, de lineares a não lineares, e até mesmo modelos de redes neurais avançados. Essas descobertas abrem a porta para melhores previsões financeiras em todos os níveis.
“As descobertas confirmam a validade da teoria e encorajam a comunidade científica a aprofundar esta nova e excitante intersecção entre matemática e finanças”, concluiu Souto.
Referência: “Dependência topológica da cauda: evidências da previsão da volatilidade realizada” por Hugo Gobato Souto, 14 de outubro de 2023, O Jornal de Finanças e Ciência de Dados.
DOI: 10.1016/j.jfds.2023.100107