
Os pesquisadores fizeram um avanço significativo na geometria espectral ao provar um caso especial da conjectura de Pólya relacionado aos autovalores de um disco. O seu trabalho, combinando elegância teórica com potenciais aplicações práticas, destaca o valor universal e a beleza artística da investigação matemática. Crédito: SciTechDaily.com
Um professor e seus colaboradores provaram a conjectura de Pólya para os autovalores de um disco, um problema complicado em matemática.
É possível deduzir a forma de um tambor a partir dos sons que ele emite?
Este é o tipo de pergunta que Iosif Polterovich, professor do Departamento de Matemática e Estatística da Universidade de Montreal, gosta de fazer. Polterovich usa geometria espectral, um ramo da matemática, para compreender fenômenos físicos que envolvem a propagação de ondas.
Avanço na conjectura matemática
No verão passado, Polterovich e os seus colaboradores internacionais – Nikolay Filonov, Michael Levitin e David Sher – provaram um caso especial de uma famosa conjectura em geometria espectral formulada em 1954 pelo eminente matemático húngaro-americano George Pólya.
A conjectura refere-se à estimativa das frequências de um tambor redondo ou, em termos matemáticos, dos autovalores de um disco.
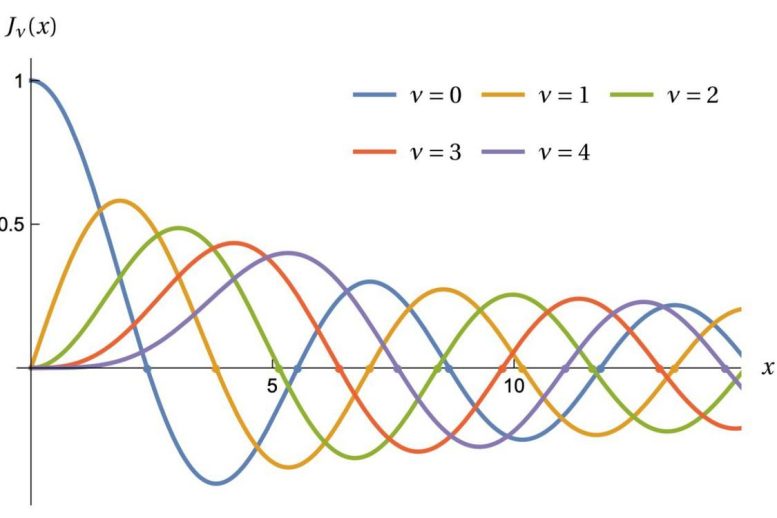
Este gráfico mostra funções de Bessel, onde os pontos correspondem às frequências dos sons de um tambor redondo. Crédito: Michael Levitin
O próprio Pólya confirmou sua conjectura em 1961 para domínios que ladeiam um plano, como triângulos e retângulos. Até o ano passado, a conjectura era conhecida apenas para esses casos. O disco, apesar de sua aparente simplicidade, permaneceu indefinido.
“Imagine um piso infinito coberto com ladrilhos do mesmo formato que se encaixam para preencher o espaço”, disse Polterovich. “Pode ser ladrilhado com quadrados ou triângulos, mas não com discos. Na verdade, um disco não é um bom formato para ladrilhos.”
A universalidade e o impacto da matemática
Em artigo publicado em julho de 2023 na revista matemática Descobertas matemáticasos pesquisadores mostram que a conjectura de Pólya é verdadeira para o disco, um caso considerado particularmente desafiador.
Embora seu resultado seja essencialmente de valor teórico, seu método de prova tem aplicações em matemática computacional e computação numérica. Os autores estão agora investigando esse caminho.

Joseph Polterovich
“Embora a matemática seja uma ciência fundamental, é semelhante aos esportes e às artes em alguns aspectos”, disse Polterovich.
“Tentar provar uma conjectura de longa data é um esporte. Encontrar uma solução elegante é uma arte. E, em muitos casos, belas descobertas matemáticas revelam-se úteis – basta encontrar a aplicação certa.”
Referência: “A conjectura de Pólya para bolas euclidianas” por Nikolay Filonov, Michael Levitin, Iosif Polterovich e David A. Sher, 5 de junho de 2023, Descobertas matemáticas.
DOI: 10.1007/s00222-023-01198-1